How to build a Grapheme-to-Phoneme (G2P) model using PyTorch
introduction¶
Grapheme-to-Phoneme (G2P) model is one of the core components of a typical Text-to-Speech (TTS) system, e.g. WaveNet and Deep Voice. In this notebook, we will try to replicate the Encoder-decoder LSTM model from the paper https://arxiv.org/abs/1506.00196.
Throughout this tutorial, we will learn how to:
- Implement a sequence-to-sequence (seq2seq) model
- Implement global attention into seq2seq model
- Use beam-search decoder
- Use Levenshtein distance to compute phoneme-error-rate (PER)
- Use torchtext package
setup¶
First, we will import necessary modules. You can install PyTorch as suggested in its main page. To install torchtext, simply call
pip install git+https://github.com/pytorch/text.git
Due to this bug, it is important to update your torchtext to the lastest version (using the above installing command is enough).
import argparse
import os
import time
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
import torch.optim as optim
from torch.nn.utils import clip_grad_norm
import torchtext.data as data
parser = {
'data_path': '../data/cmudict/',
'epochs': 50,
'batch_size': 100,
'max_len': 20, # max length of grapheme/phoneme sequences
'beam_size': 3, # size of beam for beam-search
'd_embed': 500, # embedding dimension
'd_hidden': 500, # hidden dimension
'attention': True, # use attention or not
'log_every': 100, # number of iterations to log and validate training
'lr': 0.007, # initial learning rate
'lr_decay': 0.5, # decay lr when not observing improvement in val_loss
'lr_min': 1e-5, # stop when lr is too low
'n_bad_loss': 5, # number of bad val_loss before decaying
'clip': 2.3, # clip gradient, to avoid exploding gradient
'cuda': True, # using gpu or not
'seed': 5, # initial seed
'intermediate_path': '../intermediate/g2p/', # path to save models
}
args = argparse.Namespace(**parser)
Next, we need to download the data. We will use the free CMUdict dataset. The seed 5 is used to generate random numbers for the purpose of replicating the result. However, we still observe distinct scores for different runs of the notebook.
args.cuda = args.cuda and torch.cuda.is_available()
if not os.path.isdir(args.intermediate_path):
os.makedirs(args.intermediate_path)
if not os.path.isdir(args.data_path):
URL = "https://github.com/cmusphinx/cmudict/archive/master.zip"
!wget $URL -O ../data/cmudict.zip
!unzip ../data/cmudict.zip -d ../data/
!mv ../data/cmudict-master $args.data_path
torch.manual_seed(args.seed)
if args.cuda:
torch.cuda.manual_seed(args.seed)
model¶
Now, it is time to define our model. The following figure (taken from the paper) is a two layer Encoder-Decoder LSTM model (which is a variant of Sequence-to-Sequence model). To understand how LSTM works, we can look at the excellent blog post http://colah.github.io/posts/2015-08-Understanding-LSTMs/. Each rectangle in the figure will be an LSTMCell in our code.
Before looking into the code, we need to review some PyTorch modules and functions:
- nn.Embedding: a lookup table to convert indices to vectors. Theoretically, it does one-hot encoding followed by a fully connected layer (with no bias).
- nn.Linear: nothing but a fully connected layer.
- nn.LSTMCell: a long short-term memory cell, which is mentioned above.
- size: get the size of tensor.
- unsqueeze: create a new dimension (with size 1) for a tensor.
- squeeze: drop a (size 1) dimension of a tensor.
- chunk: split a tensor along a dimension into smaller-size tensors. There is also the function split which help us obtain the same effect.
- stack: concatenate a list of tensors along a new dimension. If we want to concatenate a long a "known" dimension, then we can use cat function.
- bmm: batch matrix multiplication.
- index_select: select values of a tensor by providing indices.
- F.softmax, F.tanh: non-linear activation functions.
PyTorch's implementation of the encoder is quite straight forward. If you are not familiar with PyTorch, we recommend you to look at the official tutorials. It is noted that the dimension for input tensor x_seq is seq_len x batch_size. After embedding, we get a tensor of size seq_len x batch_size x vector_dim, not batch_size x seq_len x vector_dim. For us, this order of dimensions is useful for getting subsequence tensor, or an element of the sequence (for examples, to get the first element of the sequence x_seq, we just take x_seq[0]). Note that this is also the default order of input tensor for any recurrent module in PyTorch.
class Encoder(nn.Module):
def __init__(self, vocab_size, d_embed, d_hidden):
super(Encoder, self).__init__()
self.embedding = nn.Embedding(vocab_size, d_embed)
self.lstm = nn.LSTMCell(d_embed, d_hidden)
self.d_hidden = d_hidden
def forward(self, x_seq, cuda=False):
o = []
e_seq = self.embedding(x_seq) # seq x batch x dim
tt = torch.cuda if cuda else torch # use cuda tensor or not
# create initial hidden state and initial cell state
h = Variable(tt.FloatTensor(e_seq.size(1), self.d_hidden).zero_())
c = Variable(tt.FloatTensor(e_seq.size(1), self.d_hidden).zero_())
for e in e_seq.chunk(e_seq.size(0), 0):
e = e.squeeze(0)
h, c = self.lstm(e, (h, c))
o.append(h)
return torch.stack(o, 0), h, c
Next, we want to implement the decoder with attention mechanism. The article http://distill.pub/2016/augmented-rnns/ explains very well the idea behind the notion "attention". Here we use dot global attention from the paper https://arxiv.org/abs/1508.04025. (The following figure is taken from this blog.)
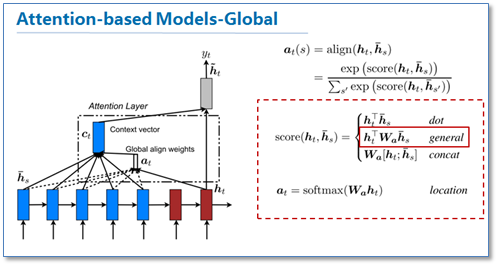
# Based on https://github.com/OpenNMT/OpenNMT-py
class Attention(nn.Module):
"""Dot global attention from https://arxiv.org/abs/1508.04025"""
def __init__(self, dim):
super(Attention, self).__init__()
self.linear = nn.Linear(dim*2, dim, bias=False)
def forward(self, x, context=None):
if context is None:
return x
assert x.size(0) == context.size(0) # x: batch x dim
assert x.size(1) == context.size(2) # context: batch x seq x dim
attn = F.softmax(context.bmm(x.unsqueeze(2)).squeeze(2))
weighted_context = attn.unsqueeze(1).bmm(context).squeeze(1)
o = self.linear(torch.cat((x, weighted_context), 1))
return F.tanh(o)
Note that if we do not want to add attention to the decoder, then simply set the args.attention to False. In our experiment, adding attention gave us worse result.
class Decoder(nn.Module):
def __init__(self, vocab_size, d_embed, d_hidden):
super(Decoder, self).__init__()
self.embedding = nn.Embedding(vocab_size, d_embed)
self.lstm = nn.LSTMCell(d_embed, d_hidden)
self.attn = Attention(d_hidden)
self.linear = nn.Linear(d_hidden, vocab_size)
def forward(self, x_seq, h, c, context=None):
o = []
e_seq = self.embedding(x_seq)
for e in e_seq.chunk(e_seq.size(0), 0):
e = e.squeeze(0)
h, c = self.lstm(e, (h, c))
o.append(self.attn(h, context))
o = torch.stack(o, 0)
o = self.linear(o.view(-1, h.size(1)))
return F.log_softmax(o).view(x_seq.size(0), -1, o.size(1)), h, c
The following G2P model is a combination of the above encoder and decoder into an end-to-end setting. We also use beam search to find the best converted phoneme sequence. To learn more about beam search, the following clip is helpful. In the implementation of beam search, we deal with one sequence at a time (try to find the phoneme sequence ending with token eos). So we have to make sure batch_size == 1.
class G2P(nn.Module):
def __init__(self, config):
super(G2P, self).__init__()
self.encoder = Encoder(config.g_size, config.d_embed,
config.d_hidden)
self.decoder = Decoder(config.p_size, config.d_embed,
config.d_hidden)
self.config = config
def forward(self, g_seq, p_seq=None):
o, h, c = self.encoder(g_seq, self.config.cuda)
context = o.t() if self.config.attention else None
if p_seq is not None: # not generate
return self.decoder(p_seq, h, c, context)
else:
assert g_seq.size(1) == 1 # make sure batch_size = 1
return self._generate(h, c, context)
def _generate(self, h, c, context):
beam = Beam(self.config.beam_size, cuda=self.config.cuda)
# Make a beam_size batch.
h = h.expand(beam.size, h.size(1))
c = c.expand(beam.size, c.size(1))
context = context.expand(beam.size, context.size(1), context.size(2))
for i in range(self.config.max_len): # max_len = 20
x = beam.get_current_state()
o, h, c = self.decoder(Variable(x.unsqueeze(0)), h, c, context)
if beam.advance(o.data.squeeze(0)):
break
h.data.copy_(h.data.index_select(0, beam.get_current_origin()))
c.data.copy_(c.data.index_select(0, beam.get_current_origin()))
tt = torch.cuda if self.config.cuda else torch
return Variable(tt.LongTensor(beam.get_hyp(0)))
utils¶
The following class is the implementation of Beam search. Note that the special tokens pad, bos, eos have to match the corresponding tokens in phoneme dictionary.
# Based on https://github.com/MaximumEntropy/Seq2Seq-PyTorch/
class Beam(object):
"""Ordered beam of candidate outputs."""
def __init__(self, size, pad=1, bos=2, eos=3, cuda=False):
"""Initialize params."""
self.size = size
self.done = False
self.pad = pad
self.bos = bos
self.eos = eos
self.tt = torch.cuda if cuda else torch
# The score for each translation on the beam.
self.scores = self.tt.FloatTensor(size).zero_()
# The backpointers at each time-step.
self.prevKs = []
# The outputs at each time-step.
self.nextYs = [self.tt.LongTensor(size).fill_(self.pad)]
self.nextYs[0][0] = self.bos
# Get the outputs for the current timestep.
def get_current_state(self):
"""Get state of beam."""
return self.nextYs[-1]
# Get the backpointers for the current timestep.
def get_current_origin(self):
"""Get the backpointer to the beam at this step."""
return self.prevKs[-1]
def advance(self, workd_lk):
"""Advance the beam."""
num_words = workd_lk.size(1)
# Sum the previous scores.
if len(self.prevKs) > 0:
beam_lk = workd_lk + self.scores.unsqueeze(1).expand_as(workd_lk)
else:
beam_lk = workd_lk[0]
flat_beam_lk = beam_lk.view(-1)
bestScores, bestScoresId = flat_beam_lk.topk(self.size, 0,
True, True)
self.scores = bestScores
# bestScoresId is flattened beam x word array, so calculate which
# word and beam each score came from
prev_k = bestScoresId / num_words
self.prevKs.append(prev_k)
self.nextYs.append(bestScoresId - prev_k * num_words)
# End condition is when top-of-beam is EOS.
if self.nextYs[-1][0] == self.eos:
self.done = True
return self.done
def get_hyp(self, k):
"""Get hypotheses."""
hyp = []
# print(len(self.prevKs), len(self.nextYs), len(self.attn))
for j in range(len(self.prevKs) - 1, -1, -1):
hyp.append(self.nextYs[j + 1][k])
k = self.prevKs[j][k]
return hyp[::-1]
Levenshtein distance is used to compute phoneme-error-rate (PER) for phoneme sequences (similar to word-error-rate for word sequences). In the paper, there is another metric named word-error-rate, which is obtained by calculating the number of wrong predictions. For example, the phoneme sequence "S W AY1 G ER0 D" is a wrong prediction for the word "sweigard" (real phoneme sequence is "S W EY1 G ER0 D"). Please not to be confused between these two metrics which have the same name.
# Based on https://github.com/SeanNaren/deepspeech.pytorch/blob/master/decoder.py.
import Levenshtein # https://github.com/ztane/python-Levenshtein/
def phoneme_error_rate(p_seq1, p_seq2):
p_vocab = set(p_seq1 + p_seq2)
p2c = dict(zip(p_vocab, range(len(p_vocab))))
c_seq1 = [chr(p2c[p]) for p in p_seq1]
c_seq2 = [chr(p2c[p]) for p in p_seq2]
return Levenshtein.distance(''.join(c_seq1),
''.join(c_seq2)) / len(c_seq2)
The following function helps to adjust learning rate for optimizer. Learning rate will be decayed if we do not see any improvement of the loss after args.n_bad_loss iterations.
def adjust_learning_rate(optimizer, lr_decay):
for param_group in optimizer.param_groups:
param_group['lr'] *= lr_decay
train¶
The following functions will be used to train model, validate model (using early stopping). Then we apply the final model for test data to get WER and PER (using test function). Finally, the show function will display a few examples for us.
def train(config, train_iter, model, criterion, optimizer, epoch):
global iteration, n_total, train_loss, n_bad_loss
global init, best_val_loss, stop
print("=> EPOCH {}".format(epoch))
train_iter.init_epoch()
for batch in train_iter:
iteration += 1
model.train()
output, _, __ = model(batch.grapheme, batch.phoneme[:-1].detach())
target = batch.phoneme[1:]
loss = criterion(output.view(output.size(0) * output.size(1), -1),
target.view(target.size(0) * target.size(1)))
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm(model.parameters(), config.clip, 'inf')
optimizer.step()
n_total += batch.batch_size
train_loss += loss.data[0] * batch.batch_size
if iteration % config.log_every == 0:
train_loss /= n_total
val_loss = validate(val_iter, model, criterion)
print(" % Time: {:5.0f} | Iteration: {:5} | Batch: {:4}/{}"
" | Train loss: {:.4f} | Val loss: {:.4f}"
.format(time.time()-init, iteration, train_iter.iterations,
len(train_iter), train_loss, val_loss))
# test for val_loss improvement
n_total = train_loss = 0
if val_loss < best_val_loss:
best_val_loss = val_loss
n_bad_loss = 0
torch.save(model.state_dict(), config.best_model)
else:
n_bad_loss += 1
if n_bad_loss == config.n_bad_loss:
best_val_loss = val_loss
n_bad_loss = 0
adjust_learning_rate(optimizer, config.lr_decay)
new_lr = optimizer.param_groups[0]['lr']
print("=> Adjust learning rate to: {}".format(new_lr))
if new_lr < config.lr_min:
stop = True
break
def validate(val_iter, model, criterion):
model.eval()
val_loss = 0
val_iter.init_epoch()
for batch in val_iter:
output, _, __ = model(batch.grapheme, batch.phoneme[:-1])
target = batch.phoneme[1:]
loss = criterion(output.squeeze(1), target.squeeze(1))
val_loss += loss.data[0] * batch.batch_size
return val_loss / len(val_iter.dataset)
def test(test_iter, model, criterion):
model.eval()
test_iter.init_epoch()
test_per = test_wer = 0
for batch in test_iter:
output = model(batch.grapheme).data.tolist()
target = batch.phoneme[1:].squeeze(1).data.tolist()
# calculate per, wer here
per = phoneme_error_rate(output, target)
wer = int(output != target)
test_per += per # batch_size = 1
test_wer += wer
test_per = test_per / len(test_iter.dataset) * 100
test_wer = test_wer / len(test_iter.dataset) * 100
print("Phoneme error rate (PER): {:.2f}\nWord error rate (WER): {:.2f}"
.format(test_per, test_wer))
def show(batch, model):
assert batch.batch_size == 1
g_field = batch.dataset.fields['grapheme']
p_field = batch.dataset.fields['phoneme']
prediction = model(batch.grapheme).data.tolist()[:-1]
grapheme = batch.grapheme.squeeze(1).data.tolist()[1:][::-1]
phoneme = batch.phoneme.squeeze(1).data.tolist()[1:-1]
print("> {}\n= {}\n< {}\n".format(
''.join([g_field.vocab.itos[g] for g in grapheme]),
' '.join([p_field.vocab.itos[p] for p in phoneme]),
' '.join([p_field.vocab.itos[p] for p in prediction])))
prepare¶
Now, we move to the exciting part. We will create a class CMUDict based on data.Dataset from torchtext. It is recommended to read the document to understand how the Dataset works. The splits function helps us divide data into three datasets: 17/20 for training, 1/20 for validating, 2/20 for reporting final results.
The class CMUDict contains all pairs of a grapheme sequence and the corresponding phoneme sequence. Each line of the raw cmudict.dict file has the form "aachener AA1 K AH0 N ER0". We first split it into sequences aachener and AA1 K AH0 N ER0. Each of them is a sequence of data belongs to a Field (for example, a sentence is a sequence of words and word is the Field of sentences). How to tokenize these sequences is implemented in the tokenize parameters of the definition of grapheme field and phoneme field. We also add init token and end-of-sequence token as in the original paper.
g_field = data.Field(init_token='<s>',
tokenize=(lambda x: list(x.split('(')[0])[::-1]))
p_field = data.Field(init_token='<os>', eos_token='</os>',
tokenize=(lambda x: x.split('#')[0].split()))
class CMUDict(data.Dataset):
def __init__(self, data_lines, g_field, p_field):
fields = [('grapheme', g_field), ('phoneme', p_field)]
examples = [] # maybe ignore '...-1' grapheme
for line in data_lines:
grapheme, phoneme = line.split(maxsplit=1)
examples.append(data.Example.fromlist([grapheme, phoneme],
fields))
self.sort_key = lambda x: len(x.grapheme)
super(CMUDict, self).__init__(examples, fields)
@classmethod
def splits(cls, path, g_field, p_field, seed=None):
import random
if seed is not None:
random.seed(seed)
with open(path) as f:
lines = f.readlines()
random.shuffle(lines)
train_lines, val_lines, test_lines = [], [], []
for i, line in enumerate(lines):
if i % 20 == 0:
val_lines.append(line)
elif i % 20 < 3:
test_lines.append(line)
else:
train_lines.append(line)
train_data = cls(train_lines, g_field, p_field)
val_data = cls(val_lines, g_field, p_field)
test_data = cls(test_lines, g_field, p_field)
return (train_data, val_data, test_data)
filepath = os.path.join(args.data_path, 'cmudict.dict')
train_data, val_data, test_data = CMUDict.splits(filepath, g_field, p_field,
args.seed)
To make the dictionaries for grapheme field and phoneme field, we use the function build_vocab. Read its definition to get more information.
g_field.build_vocab(train_data, val_data, test_data)
p_field.build_vocab(train_data, val_data, test_data)
Now, we will make Iterator from our datasets. These iterators will help us get data in batch. The BucketIterator will make the sequences in each batch have similar length while still preserves the randomness.
device = None if args.cuda else -1 # None is current gpu
train_iter = data.BucketIterator(train_data, batch_size=args.batch_size,
repeat=False, device=device)
val_iter = data.Iterator(val_data, batch_size=1,
train=False, sort=False, device=device)
test_iter = data.Iterator(test_data, batch_size=1,
train=False, shuffle=True, device=device)
Now, it is time to create the model.
config = args
config.g_size = len(g_field.vocab)
config.p_size = len(p_field.vocab)
config.best_model = os.path.join(config.intermediate_path,
"best_model_adagrad_attn.pth")
model = G2P(config)
criterion = nn.NLLLoss()
if config.cuda:
model.cuda()
criterion.cuda()
optimizer = optim.Adagrad(model.parameters(), lr=config.lr) # use Adagrad
run¶
We start to train our model. It will be stopped if there is no observation on the improvement of validation loss. It take around 10 minutes for each epoch (trained on GTX 1060).
if 1 == 1: # change to True to train
iteration = n_total = train_loss = n_bad_loss = 0
stop = False
best_val_loss = 10
init = time.time()
for epoch in range(1, config.epochs+1):
train(config, train_iter, model, criterion, optimizer, epoch)
if stop:
break
test¶
We also want to report WER and PER. In this notebook, we use attention. Setting args.attention to False to disable it, which will improve the results.
model.load_state_dict(torch.load(config.best_model))
test(test_iter, model, criterion)
Now we display 10 examples. The first line is the word, the second line is its 'true' phoneme, and the third line is our prediction.
test_iter.init_epoch()
for i, batch in enumerate(test_iter):
show(batch, model)
if i == 10:
break
As you can see, the result is quite good. Happy learning!
acknowledgement¶
This tutorial is done under my study with Hoang Le and Hoang Nguyen. Thank you very much for your help!
Comments
Comments powered by Disqus